PID Controllers

In the world of robotics and game engines, it is common that a physics object needs to be moved or articulated to a precise location or rotation. Such objects are commonly referred as rigidbodies. In order to move these rigidbodies, a force or torque needs to be applied to reach the object’s target.

A common way to move physics objects in Unity is to use Rigidbody.AddForce, or by adjusting the rigidbody’s velocity directly, although Unity advises against this (unless you know what you’re doing).

Rigidbody-Velocity: In most cases you should not modify the velocity directly, as this can result in unrealistic behaviour - use AddForce instead Do not set the velocity of an object every physics step, this will lead to unrealistic physics simulation. A typical usage is where you would change the velocity is when jumping in a first person shooter, because you want an immediate change in velocity.

Although this is main method of moving rigidbodies, forces need to be calculated each step to ensure objects reach their destination as fast as desired, without overshooting the target.

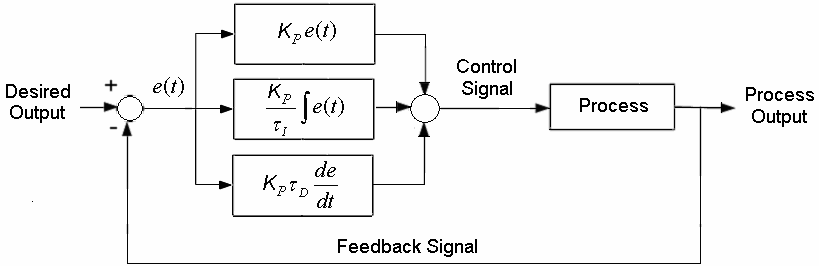
In modern robotics machines need to be articulated to precise positions and rotations for maximum efficiency as well as safety. The PID controller is a simple solution to adjust rigidbodies in real time with little oversight needed once setup properly. A pid controller is a closed feedback loop which input the current status of the rigidbody every step, and then provides a force in order to reach the target, and then provides feedback into the loop for a calculation in the next step.

I won’t go too heavy into the math, instead will provide a brief overview with example:

Vector3 Controller() {
  Vector3 proportion = target.position - current.position;
  
  this._integral += (error * deltaTime);

  Vector3 derivative = (error - errorPrev) / deltaTime;
  Vector3 output = (Kp * error) + (Ki * this._integral) + (Kd * derivative);

  this.errorPrev = error;

  return output;
}

In the above code, there are three primary areas of focus which makes the PID controller work.

• Proportion, also referred to as the margin of error, is the calculation of how far away an object is from it’s target.
• Integral accounts for error values in the previous step, which will then add to the current step to help midigate the margin of error.
• Derivative, to put shortly, is the dampening factor of the process. A higher derivative value will give a higher dampening value. Kp, Ki, and Kd are tuning paremeters which affect their respective variable.

This is a simple example of a PID, which needs to be tuned at runtime to achieve desired speed and damping. This can be expanded to include limiting the maximum forces applied, account for inertia tensors, integration into configurable joints, and be used to predict future movements of the object for better automation and force control. These topics may be expanded upon later.

• Thanks to Dr. Kaplanoglu.